Conjetura de Beal
La conjetura de Beal es una conjetura en teoría de números propuesta por Andrew Beal sobre 1993; una conjetura similar fue sugerida independientemente en esas fechas por Andrew Granville.
Mientras investigaba generalizaciones del último teorema de Fermat en 1993, Beal formuló la siguiente conjetura:
Si
donde A, B, C, x, y, z son enteros positivos con x, y, z > 2 entonces A, B, y C deben tener un factor común primo.
Beal ha ofrecido un premio de 1000000 US$ por una demostración de esta conjetura o por un contraejemplo.1
Para ilustrar, la solución 33 + 63 = 35 tiene sus bases con un factor común 3, y la solución 76 + 77 = 983 tiene las bases con un factor común 7. De hecho, la ecuación tiene infinitas soluciones, incluyendo, por ejemplo
para cualquier  ,
,  ,
,  . Pero tal solución de la ecuación no es un contraejemplo de la conjetura, puesto que todas las bases tienen el factor
. Pero tal solución de la ecuación no es un contraejemplo de la conjetura, puesto que todas las bases tienen el factor  en común.
en común.
 ,
,  ,
,  . Pero tal solución de la ecuación no es un contraejemplo de la conjetura, puesto que todas las bases tienen el factor
. Pero tal solución de la ecuación no es un contraejemplo de la conjetura, puesto que todas las bases tienen el factor  en común.
en común.
El ejemplo 73 + 132 = 29 muestra que la conjetura es falsa si uno de los exponentes es igual a 2.
También se cuenta con el ejemplo fácil de 24 + 42 = 25
Mediante búsqueda por ordenador, muy acelerada, mediante la ayuda de aritmética modular, esta conjetura ha sido verificada para todo valor de las seis variables hasta 1000.2 Así, en un contraejemplo, al menos una de las variables debe de ser mayor que 1000.
Una variación de la conjetura donde x, y, z (en lugar de A, B, C) debe de tener un factor común primo no es verdad. Véase, por ejemplo  .
.
 .
.
La conjetura de Beal es una generalización del último teorema de Fermat, que corresponde al caso  . Si
. Si  con
con  ; entonces, o las bases son coprimas o comparten un factor común. Si estas comparten un factor común, se puede sacar de cada una de ellas para obtener una ecuación más pequeña, con bases coprimas.
; entonces, o las bases son coprimas o comparten un factor común. Si estas comparten un factor común, se puede sacar de cada una de ellas para obtener una ecuación más pequeña, con bases coprimas.
 . Si
. Si  con
con  ; entonces, o las bases son coprimas o comparten un factor común. Si estas comparten un factor común, se puede sacar de cada una de ellas para obtener una ecuación más pequeña, con bases coprimas.
; entonces, o las bases son coprimas o comparten un factor común. Si estas comparten un factor común, se puede sacar de cada una de ellas para obtener una ecuación más pequeña, con bases coprimas.
La conjetura no es válida sobre un dominio más grande de enteros gaussianos. Después de que se ofreciera un precio de 50$ por un contraejemplo, Fred W. Helenius proporcionó el siguiente: (−2 + i)3 + (−2 − i)3 = (1 + i)4.3
Último teorema de Fermat
En teoría de números, el último teorema de Fermat, o teorema de Fermat-Wiles, es uno de los teoremas más famosos en la historia de la matemática. Utilizando la notación moderna, se puede enunciar de la siguiente manera:
|
Nótese que n es un entero mayor que 2, y x, y, z, no nulos. Es decir, ni x=0, ni y=0, ni z=0.
El teorema fue conjeturado por Pierre de Fermat en 1637, pero no fue demostrado hasta 1995 por Andrew Wiles ayudado por el matemático Richard Taylor. La búsqueda de una demostración estimuló el desarrollo de la teoría algebraica de números en el siglo XIX y la demostración del teorema de la modularidad en el siglo XX.
Introducción Histórica
Pierre de Fermat escribió en el margen de su ejemplar de la Arithmetica de Diofanto, traducido por Claude Gaspar Bachet, en el problema que trata sobre escribir un número cuadrado como suma de dos cuadrados (es decir, encontrar ternas pitagóricas):
Cubum autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet. Es imposible descomponer un cubo en dos cubos, un bicuadrado en dos bicuadrados, y en general, una potencia cualquiera, aparte del cuadrado, en dos potencias del mismo exponente. He encontrado una demostración realmente admirable, pero el margen del libro es muy pequeño para ponerla.
Pierre Fermat
El primer matemático que consiguió avanzar sobre este teorema fue el propio Fermat, que demostró el caso n=4 usando la técnica del descenso infinito, una variante del principio de inducción.
Leonhard Euler
Leonhard Euler demostró el caso n = 3. El 4 de agosto de 1735 Euler escribió a Goldbach reclamando tener una demostración para el caso n = 3. En Álgebra (1770) se encontró una falacia en la demostración de Euler. Corregirla directamente era demasiado difícil, pero otros aportes anteriores de Euler permitían encontrar una solución correcta por medios más simples. Por esto se consideró que Euler había demostrado ese caso. Del análisis de la demostración fallida de Euler surgió la evidencia de que ciertos conjuntos de números complejos no se comportaban de igual manera que los enteros.
Sophie Germain
El siguiente mayor paso fue hecho por la matemática Sophie Germain. Un caso especial dice que si p y 2p + 1 son ambos primos, entonces la expresión de la conjetura de Fermat para la potencia p implica que uno de los x, y ó z es divisible por p. En consecuencia la conjetura se divide en dos casos:
- Caso 1: Ninguno de los x, y, z es divisible por p.
- Caso 2: Uno y sólo uno de x, y, z es divisible por p.
Sophie Germain probó el caso 1 para todo p menor que 100 y Adrien-Marie Legendre extendió sus métodos a todos los números menores que 197. Aquí se encontró que el caso 2 no estaba demostrado ni siquiera para p = 5, por lo que fue evidente que era en el caso 2 en el que había que concentrarse. Este caso también se dividía entre varios casos posibles.
Ernst Kummer
No fue hasta 1825 que Peter Gustav Lejeune Dirichlet y Legendre generalizaron para n=5 la demostración de Euler.Lamé demostró el caso n=7 en 1839.
Entre 1844 y 1846 Ernst Kummer demostró que la factorización no única podía ser salvada mediante la introducción denúmeros complejos ideales. Un año después Kummer afirma que el número 37 no es un primo regular (Ver: Números de Bernoulli). Luego se encuentra que tampoco 59 y 67 lo son. Kummer, Mirimanoff, Wieferich, Furtwänger, Vandiver y otros extienden la investigación a números más grandes. En 1915 Jensen demuestra que existen infinitos primos irregulares. La investigación se estanca por esta vía de la divisibilidad, a pesar de que se logran comprobaciones para nmenor o igual a 4.000.000.
Andrew Wiles
En el año 1995 el matemático Andrew Wiles, en un artículo de 98 páginas publicado en Annals of mathematics, demostró el caso semiestable del Teorema de Taniyama-Shimura, anteriormente una conjetura, que engarza las formas modulares y las curvas elípticas. De este trabajo, combinado con ideas de Frey y con el Teorema de Ribet, se desprende la demostración del Último Teorema de Fermat.3 Aunque una versión anterior (no publicada) del trabajo de Wiles contenía un error, este pudo ser corregido en la versión publicada, que consta de dos artículos, el segundo en colaboración con el matemático Richard Taylor. En estos trabajos por primera vez se establecen resultados de modularidad a partir de modularidad residual, por lo cual los resultados del tipo de los probados por Wiles y Taylor son denominados "Teoremas de Levantamiento Modular". En la actualidad resultados de este tipo, mucho más generales y poderosos, han sido probados por varios matemáticos: además de generalizaciones probadas por Wiles en colaboración con C. Skinner y de Taylor en colaboración con M. Harris, los más generales en la actualidad se deben a Mark Kisin. En el trabajo de 1995 de Wiles se abrió una nueva vía, prácticamente una nueva área: la de la modularidad. Con estas técnicas de las que este trabajo fue pionero, más recientemente se han resuelto otras importantes conjeturas, como la Conjetura de Serre y la de Sato-Tate. Curiosamente, la resolución de los primeros casos de la Conjetura de Serre (trabajos de Khare, Wintenberger y Dieulefait), como observara el propio Serre al formular la conjetura, permite una nueva demostración del Último Teorema de Fermat.4
Los trabajos de Wiles por lo tanto tienen una importancia que trasciende ampliamente su aplicación al Último Teorema de Fermat, se consideran centrales en la Geometría Aritmética moderna y se espera que sigan jugando un rol vital en la demostración de resultados de modularidad que se enmarcan en el Programa de Langlands.
Pequeño Teorema de Fermat
El pequeño teorema de Fermat es uno de los teoremas clásicos de teoría de números relacionado con la divisibilidad. Se formula de la siguiente manera:
|
Aunque son equivalentes, el teorema suele ser presentado de esta otra forma:
|
Esto quiere decir que, si se eleva un número a a la p-ésima potencia y al resultado se le resta a, lo que queda es divisible por p (véase aritmética modular). Su interés principal está en su aplicación al problema de la primalidad y en criptografía.
Este teorema no tiene nada que ver con el legendario último teorema de Fermat, que fue sólo una conjetura durante 350 años y finalmente fue demostrado por Andrew Wiles en 1995.1
Historia
La civilización china parece que fue la primera cultura en estar interesada en la aritmética modular.2 Existe una hipótesis,3 documentada por Joseph Needham, según la cual los números de la forma 2p − 2 fueron estudiados por esta civilización.
Así pues, matemáticos chinos formularon la hipótesis (a veces conocida como hipótesis china) de que p es primo si y sólo si 2p ≡ 2 (mod p) (donde el símbolo ≡ significa congruencia según el módulo indicado). Es verdad que, si p es primo, entonces 2p ≡ 2 (mod p) (este es un caso especial del pequeño teorema de Fermat), pero el recíproco (si 2p ≡ 2 (mod p), entonces p es primo) no lo es, por lo que la hipótesis es falsa.
Se cree ampliamente que la hipótesis china fue desarrollada 2000 años antes del trabajo de Fermat en el siglo XVII. Aunque la hipótesis sea parcialmente incorrecta, es notable que pueda haber sido conocida por los matemáticos de la antigüedad. Algunos, sin embargo, sostienen que la creencia de que esta hipótesis fuera conocida hace tanto tiempo es fruto de un error de comprensión, y que se desarrolló realmente en 1872. Para más información sobre este asunto, consúltese (Ribenboim,1995).
Alrededor de 1636, Pierre de Fermat enunció el teorema. Aparece en una de sus cartas a su confidente Frénicle de Bessy, fechada el 18 de octubre de 1640, con el siguiente texto: p divide a ap-1 - 1 cuando p sea primo y a sea coprimo con p.4
Aunque actualmente lo conozcamos como pequeño teorema de Fermat, lo cierto es que hasta el siglo XX fue conocido como teorema de Fermat, como recoge por ejemplo Carl Friedrich Gauss en su libro Disquisitiones arithmeticae.5 El términopequeño teorema de Fermat, tal como lo conocemos actualmente, fue usado por primera vez por el matemático alemán Kurt Hensel en 1913 en su libro Zahlentheorie.6
Für jede endliche Gruppe besteht nun ein Fundamentalsatz, welcher der kleine Fermatsche Satz genannt zu werden pflegt, weil ein ganz spezieller Teil desselben zuerst von Fermat bewiesen worden ist.
He aquí el teorema fundamental que se cumple en cada grupo finito, llamado habitualmente pequeño teorema de Fermat, porque Fermat fue el primero en probar una parte especial de él.
Demostración
Fermat estableció tal resultado en una carta a Frénicle de Bessy, pero como era habitual en él, omitió la prueba del mismo:4
Tout nombre premier mesure infailliblement une des puissances -1 de quelque progression que ce soit, et l’exposant de la dite puissance est sous-multiple du nombre premier donné -1. (...) Et cette proposition est généralement vraie en toutes progressions et en tous nombres premiers; de quoi je vous envoierois la démonstration, si je n'appréhendois d'être trop long. Todo número primo mide una de las potencias menos uno de cualquier progresión en la que el exponente es un múltiplo del primo dado menos uno. (...) Y esta proposición es generalmente cierta para todas las progresiones y todos los números primos; le enviaría la prueba, si no temiese que es demasiado larga. Pierre de Fermat
La primera demostración publicada se debe a Leonhard Euler en 1736 en un artículo titulado Theorematum Quorundam ad Números Primos Spectantium Demonstratio.7 Daría otras dos demostraciones más a lo largo de su vida,8 aunque era la primera de todas ellas la misma que había en un manuscrito personal de Gottfried Leibniz, escrito sobre 1683 y que nunca llegó a publicar.9 Gauss publicaría otra prueba más en su libroDisquisitiones arithmeticae en 1801.5 10
La prueba original de Euler (y Leibniz) es sencilla, en términos de comprensión lógica, ya que sólo utiliza métodos elementales que una persona con nociones básicas de álgebra puede entender. Su demostración se basa en el principio de inducción, que consiste en demostrar que si cierta propiedad P de los números naturales se cumple para n y también se cumple para n+1, entonces se cumple para todo n.11 Es fácil ver que si se cumple para n, y para n+1, también se cumple para n+2, n+3, etc. ya que, llamando como n1 a n+1, se cumple para n1 y n1+1, por tanto, para n, n+1 y n+2, y así sucesivamente.
Para la demostración también se utiliza la propiedad de que si p es un número primo, entonces el coeficiente binomial  es divisible por p, para todo n, tal que 1≤ n<p. Esto es así puesto que el coeficiente binomialse define como:
es divisible por p, para todo n, tal que 1≤ n<p. Esto es así puesto que el coeficiente binomialse define como:
 es divisible por p, para todo n, tal que 1≤ n<p. Esto es así puesto que el coeficiente binomialse define como:
es divisible por p, para todo n, tal que 1≤ n<p. Esto es así puesto que el coeficiente binomialse define como:
Donde el signo ! corresponde al factorial de un número, que indica la multiplicación de todos los números naturales menores o iguales a dicho número, por ejemplo, p! = p·(p-1)·(p-2)·...·2·1. Puesto que en eldenominador, los factoriales de los números involucran números que son menores que el número primo p, éstos no pueden contener p ni dividir al número primo p del numerador, así pues, el coeficiente es divisible porp.
Dicho esto, la demostración consiste en los siguientes pasos:
- Supongamos que

- Utilizamos el binomio de Newton para expandir la potencia (n + 1)p:
- Agrupando factores y reordenando la identidad:
- Por hipótesis, hemos supuesto que np - n es divisible por p, y dado que todos los términos del sumatorio del miembro de la derecha son divisibles por p, tenemos que p divide a (n + 1)p - (n + 1).
- Ahora bien, 1p - 1 es divisible por p, por lo tanto 2p - 2 también es divisible por p, y así sucesivamente.
Ejemplos:
A continuación se muestran algunos ejemplos del teorema:
- 53 − 5 = 120 es divisible por 3.
- 72 − 7 = 42 es divisible por 2.
- 25 − 2 = 30 es divisible por 5.
- (−3)7 + 3 = − 2.184 es divisible por 7.
- 297 − 2 = 158.456.325.028.528.675.187.087.900.670 es divisible por 97.
Aplicaciones
Las aplicaciones son numerosas, particularmente en criptografía. No obstante, hay ejemplos clásicos de aplicaciones del teorema en matemáticas puras, sobre todo, relacionadas con el problema de la primalidad.
Aplicaciones Teóricas
El pequeño teorema de Fermat se ha utilizado históricamente para analizar la descomposición en producto de factores primos de ciertos enteros. Así, Fermat escribió a Marin Mersenne:12
Vous me demandez si le nombre 100.895.598.169 est premier ou non, et une méthode pour découvrir, dans l'espace d'un jour, s'il est premier ou composé. A cette question, je réponds que ce nombre est composé et se fait du produit de ces deux: 898.423 et 112.303, qui sont premiers.
Usted me pregunta si el número 100.895.598.169 es primo o no, y un método para descubrir, en el plazo de un día, si es primo o compuesto. A esta pregunta, yo le respondo que este número es compuesto y que se obtiene del producto de estos dos: 898.423 y 112.303, que son primos.
Pierre de Fermat
Utilizando un método análogo, Euler invalidó la única conjetura falsa de Fermat, es decir, que los números de Fermat no son todos primos.13
Este teorema también se ha utilizado para demostrar resultados de la teoría de números algebraicos, como el teorema de Herbrand-Ribet. Ha sobrepasado el ámbito estricto de la aritmética, con una utilización para el estudio de los puntos fijos del Endomorfismo de Frobenius, por ejemplo.
Criptografía Asimétrica
La criptografía con clave pública corresponde a un código que se agrega para asegurar la confidencialidad de los mensajes con la ayuda de dos claves criptográficas. Una, que permite cifrar el mensaje, es pública. La otra, que tiene como objetivo el descifrado, es privada.
Una importante familia de códigos asimétricos utiliza la tecnología llamada RSA. La clave secreta está determinada por la descomposición de un número entero grande, a menudo de varias centenas de cifras. Éste tiene dos factores primos. Lo esencial de las técnicas industriales de principios del siglo XXI se basa en el pequeño teorema de Fermat para generar grandes números primos o para comprobar la primalidad de un número.
Test de Primalidad
El pequeño teorema de Fermat da una condición necesaria para que un número p sea primo. Es necesario que, para todo número natural a menor que p, ap-1 - 1 sea divisible por p, o sea, que ap-1 sea congruente con uno módulo p (en notación moderna como ap - 1 ≡ 1 (mod p)). Este principio es la base del test de primalidad de Fermat.14 Este test, al que asumimos una entrada n, consiste en ir probando que an-1 ≡ 1 (mod n) para una serie de valores de a, tales que sean menores que n. Si n es primo, entonces la congruencia se cumplirá siempre (condición necesaria del teorema) mientras que si n es compuesto, la congruencia puede no cumplirse. Si para algún valor de a (menor que n) no se cumple la congruencia, entonces n es compuesto. Una descripción de este test de forma general, en forma de algoritmo escrito en pseudocódigo, podría ser la siguiente:
| Algoritmo Test de primalidad de Fermat. |
Entrada: Un número natural n>1, el número k de veces que se ejecuta el test y nos determina la fiabilidad del test.
Salida: COMPUESTO si n es compuesto y POSIBLE PRIMO si n es un posible primo.
|
Existen numerosas variantes algorítmicas que usan como base este test. Las más conocidas son el test de primalidad de Solovay-Strassen y sobre todo el test de primalidad de Miller-Rabin.
Número Pseudoprimo
Los tests precedentes utilizan una condición necesaria pero no suficiente. Tanto es así que existen números enteros p compuestos y coprimos con a tal que a p-1 es congruente con uno modulo p, son los llamados pseudoprimos.15 Estos números tienen la peculiaridad de que pueden pasar el test de primalidad de Fermat algunas veces, siendo reconocidos como falsos primos. Existen varias clases de pseudoprimos, por ejemplo, los que cumplen que ap-1 ≡ 1 (mod p) para todos los valores dea que sean coprimos con p, siendo p compuesto se denominan números de Carmichael. El número 1729 es un ejemplo de número de Carmichael. Además existen otros pseudoprimos que sólo se cumplen para una base a concreta, por ejemplo, sia es igual a 2, 341 cumple que 2341-1 ≡ 1 (mod 341), siendo 341 claramente compuesto.
Los tests indicados en la sección anterior son todos estadísticos, en el sentido de que existe siempre una probabilidad, a veces muy débil, de que el número que ha pasado el test no es primo, debido a los pseudoprimos o al número de comprobaciones.
Generalidades
Una pequeña generalización del teorema, que se sigue de él, dice lo siguiente: si p es primo y m y n son enteros positivos con m ≡ n (mod p-1), entonces am ≡ an (mod p) para todos los enteros a.5 Expresado así, el teorema se utiliza para justificar el método de cifrado de clave pública RSA.
El pequeño teorema de Fermat se puede generalizar mediante el teorema de Euler; para cualquier módulo n y cualquier entero a coprimo con n, se tiene:
donde φ(n) es la función φ de Euler que cuenta el número de enteros entre 1 y n coprimos con n. Esta es de hecho una generalización, ya que si n = p es un número primo, entonces φ(p) = p - 1.
Aun así, todavía se puede generalizar más, como así se muestra en el teorema de Carmichael. Como antes, para cualquier módulo n y cualquier entero a coprimo con n, se tiene:
donde ahora λ(n) es la función de Carmichael.16
Número de Fermat
Un número de Fermat, nombrado en honor a Pierre de Fermat, quien fue el que formuló e investigó estos números, es un número natural de la forma:
donde n es natural. De particular interés son los números primos de Fermat.
Pierre de Fermat conjeturó que todos los números naturales de la forma
con n natural eran números primos (después de todo, los cinco primeros términos, 3 (n=0), 5 (n=1), 17 (n=2), 257 (n=3) y 65537 (n=4) lo son), pero Leonhard Euler probó que no era así en 1732. En efecto, al tomar n=5 se obtiene un número compuesto:

- 4294967297 es el número más pequeño que, siendo número de Fermat, no es primo.
Actualmente, sólo se conocen cinco números primos de Fermat, que son los que ya se conocían en tiempos del propio Fermat, y, a fecha de enero de 2009 sólo se conoce la factorización completa de los doce primeros números de Fermat (desden=0 hasta n=11). Estas son algunas de las conjeturas que existen hoy día sobre estos números:
- ¿Sólo hay cinco números primos de Fermat (3, 5, 17, 257 y 65537)?
- ¿Existen infinitos primos de Fermat?
Algunos números de Fermat y su factorización
Los nueve primeros números de Fermat son los siguientes:
| F0 | = | 21 | + | 1 | = | 3 | |
| F1 | = | 22 | + | 1 | = | 5 | |
| F2 | = | 24 | + | 1 | = | 17 | |
| F3 | = | 28 | + | 1 | = | 257 | |
| F4 | = | 216 | + | 1 | = | 65.537 | |
| F5 | = | 232 | + | 1 | = | 4.294.967.297 | |
| = | 641 × 6.700.417 | ||||||
| F6 | = | 264 | + | 1 | = | 18.446.744.073.709.551.617 | |
| = | 274.177 × 67.280.421.310.721 | ||||||
| F7 | = | 2128 | + | 1 | = | 340.282.366.920.938.463.463.374.607.431.768.211.457 | |
| = | 59.649.589.127.497.217 × 5.704.689.200.685.129.054.721 | ||||||
| F8 | = | 2256 | + | 1 | = | 115.792.089.237.316.195.423.570.985.008.687.907.853.269.984.665.640.564.039.457.584.007.913.129.639.937 | |
| = | 1.238.926.361.552.897 × 93.461.639.715.357.977.769.163.558.199.606.896.584.051.237.541.638.188.580.280.321 |
Propiedades de los números de Fermat | + | 1 | = | 115.792.089.237.316.195.423.570.985.008.687.907.853.269.984.665.640.564.039.457.584.007.913.129.639.937 | ||||||
| = |
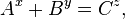
![\left[a \left(a^m + b^m\right)\right]^m + \left[b \left(a^m + b^m\right)\right]^m = \left(a^m+b^m\right)^{m+1}](http://upload.wikimedia.org/math/a/0/4/a04866e6b07e69158801f5f43762dc36.png)

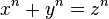




 desde
desde  hasta
hasta  haga lo siguiente:
haga lo siguiente: Función genera un número aleatorio comprendido entre
Función genera un número aleatorio comprendido entre 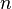 (sin incluirlos)
(sin incluirlos) entonces:
entonces: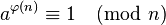

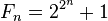




 se puede descomponer en factores primos de la forma k·2n+2 + 1, con k entero positivo.
se puede descomponer en factores primos de la forma k·2n+2 + 1, con k entero positivo.
No hay comentarios:
Publicar un comentario